2025 Fall Semester (NTU)
Table of Contents
Courses
Below are some of the courses I took (and audited) in the 2025 fall semester at NTU. Key:
- PHYS: department of Physics
- MATH: department of Mathematics
- PHYS GRAD: graduate institute of Physics
- EE GRAD: graduate institute of Electrical Engineering
- [Full Name]: others
Overview
| Course | Useful | Easy | Recommend |
|---|---|---|---|
| Quantum Field Theory II | ★★★★★ | ★★★☆☆ | ★★★★★ |
| Fundamentals of Exp. Phys. | ★★★☆☆ | ★★☆☆☆ | ★★☆☆☆ |
| Introduction to Analysis I | ★★★★★ | ★★★☆☆ | ★★★★★ |
| Introduction to ODE | ★★★★★ | ★★☆☆☆ | ★★★★☆ |
| Introduction to Geometry | ★★★☆☆ | ★★★☆☆ | ★★★☆☆ |
| Modern Poetry of Taiwan | ★★★★★ | ★★★★★ | ★★★★★ |
| Nonlinear Optics | ★★★★★ | ★★★★☆ | ★★★★☆ |
Quantum Field Theory II 量子場論 II
Lecturer: Professor Chang-Tse Hsieh 謝長澤, Chia-Hsien Shen 沈家賢
Grade: A+
Department: PHYS GRAD
Credit(s): 3
Materials:
- Self-prepared notes (main)
- Peskin, M. E.; Schroeder, D. Y. (2018). An Introduction to Quantum Field Theory [P&S]
- Weinberg, Steven. (1995). The Quantum Theory of Fields I Foundations [Weinberg]
Quantum Field Theory II is jointly instructed by Professor Chang-Tse Hsieh and Professor Chia-Hsien Shen, has no exam, and is graded based on two homework sets and a final project involving a written paper and an oral presentation.
Professor Shen held the first two lectures on the S-matrix formalism and spin-helicity formalism in person, and introduced field redefinitions in the context of the S-matrix program. The key point is that: it is usually difficult to , but if we are . Professor Hsieh then introduced the path integral formalism for interacting particles, in particular the EM field and fermions. Just around midterm weel, we had the first set of homework problems due. The problems involved some explicit calculations and fleshing details of proofs. An interesting problem was applying the Weil formula for promoting classical variables to their operator analogue to the harmonic oscillator, which involves a clever play of the BCH formula.
After midterm week, Professor Shen held another two lectures, where he introduced non-abelian gauge theories and generalized some materials from last semester, such as introducing the Ward-Takahashi identity and Faddeev-Poppov ghosts. The last few lectures of the course focused on renormalization theory, most famous of which Wilsonian renormalization, Anderson localization, and the Ising model. We introduced the idea of renormalization group (RG) flows, the beta function, and phase transitions in field theory. In the Ising model, there is no finite-temperature phase transition in 1D, but analytical (but complicated) expression for phase transition in 2D. Furthermore, beyond the critical dimension MFT can be used to derive exact values. For homework, we worked out analytically the renormalization of another system that similarly exhibits finite-temperature phase transition in 2D but not in 1D. We also made explicit calculations to check the Ward-Takahashi identity, renormalized phi-4 theory by calculating the amplitude of the sunset diagram, computed RG functions, and verified the Ward identity for scalar QCD.
My final project focused on the field theory of percolation processes, which describe many natural phenomena such as water sifting through soil, and can be applied to birth-death models in biology. Following the notes of Duminil-Copin, Bernoulli percolation was used as the introductory example to percolation theory. It turns out that percolating systems exhibit universal behavior near their critical point, and the numbers that characterize this behavior (the critical exponents) determine their universal class. This can be used to characterize many systems, including the Ising model, the liquid-gas transition, and directed percolation etc.
For both homework sets, I started working through the problems one week prior to the deadline, even though we had well over one month to complete each. Furthermore, since I spent most of my time working through math homeworks, I only began reviewing the relevant materials two weeks before the deadline, making my learning progress very unbalanced. The same happened for my term paper, and due to poor planning I was writing all the way up to the deadline, which was 23:59 on the finals week, where I was in a kebab store with my computer. Rushing through the writing process forced me to leave out some mathematical proofs and loop calculations which would make the material more readable.
For more details, you may see this post.
Fundamentals of Experimental Physics 基礎物理實驗
Lecturer: Professor Li-Min Wang 王立民
Grade: A+
Department: PHYS
Credit(s): 3
Materials:
- Course textbook
Introduction to Analysis I 分析導論 I
Lecturer: Professor 崔茂培
Grade: A+
Department: MATH
Credit(s): 5
Materials: Tao, Terence (2006). Analysis II.
The course is graded based on 12 homework sets, a midterm, and a final. The homework sets are completed and handed in in a group of three.
The pace of the lectures were very fast for an introduction course. When I took Introduction to Analysis II by Professor Chun-Chuan Chen in my freshman year, the course content paralleled that of the class content from this semester, as he spent a big portion of I constructing the real numbers from scratch. In the first week, we learned about the basic definitions of supremum/infimum and open/closed sets following awkward definitions in Tao’s book. In the second week, metric spaces and (pointwise) continuity were introduced, and later sequences, sequential and topological compactness, the Heine-Borel Theorem, and general topological spaces. The midterm exam covered materials up to chapter 2 Tao’s textbook, and included a lot of homework exercises and in-class proofs. But since there were too many problems, there was not enough time to complete the last problem on Hausdorff distance, and I got some points deducted in my solution to the problem on formal limits. After getting a few points added to the midterm exam, my score was 81, which I was confident will result in A+.
The second half of the semester, we began with the notion of sequences and their pointwise and uniform convergence. Here we introduced various techniques to show convergence and applied them to derivatives and integrals. Toward the end of chapter 3, we proved the Weierstrass approximation theorem using a variant of the kernel method presented in Rudin; however, the more general Stone-Weierstrass theorem was not presented. Then the class talked about power series, real analyticity, Abel’s theorem, and applied them to deriving properties of the zeta function, Stirling’s formula, Bernoulli numbers etc. Before finals week, we introduced Fourier theory and the Fourier theorem for periodic functions on [0,1], while in the exam we generalized this to general functions with some loosened constraints. The final exam was considerably harder than the midterm, and included only about 60 points of exercises. The remaining 50 points were new problems, and unfortunately I did not know how to solve the first problem on limits of sequences. Luckily, I did well on the exam overall.
For more details, you may see this post.
Introduction to ODE 常微分方程導論
Lecturer: Professor Tai-Chia Lin 林太家
Grade: A+
Department: MATH
Credit(s): 4
Materials:
- Hale, J, K, (1980). Ordinary Differential Equations 2e [Hale]
- King, A. C.; Billingham, J.; Otto, S.R. (2003) Differential Equations, Cambridge University Press [KBO]
- Recorded lectures by Professor Tai-Chia Lin
The course started with an introduction to ODEs, where Professor Lin gave an overview to their applications and . The first half semester followed [KBO] closely, and the first main topic was variable Coefficient, second Order, linear ODEs, where we learned reduction of order, variation of parameters, and the method of Frobenius. To complete the homework, I referred extensively to Professor Jiun-Huei Wu’s AM handouts. Then we focused on special functions including Legendre and Bessel functions, where the text was not very clearly mathematically about their properties, but focused on their applied aspects. A homework set involved showing a special case of the Markov brothers’ inequality, which turns out can be solved using generating functions. Then, before the midterm, we covered the Fourier and Laplace transforms.
The midterm exam was difficult for people who compute more slowly, though in hindsight, this should already have been anticipated from the five homework assignments. The exam consisted of nine problems. The first few involved fairly heavy computations, but they were all problems we had practiced before. From Problem 6 onward, however, it became more difficult to work through the solution. The first of these required solving a second-order differential equation using the Laplace transform and then computing the inverse transform. However, the inhomogeneous term was a piecewise function, and finding the inverse transform involved manually performing partial fraction decomposition on four expressions of the form 1/(s-2)^2(s+3)^2. The decomposition produced nearly twenty terms (fortunately, I believe I did this part correctly). The next problem covered material that we had all assumed would not appear on the exam: finding the general solution of a nonhomogeneous Bessel equation. To our surprise, it was worth 15 points, leaving no choice but to grind through it using the most basic method. The final problem involved solving the axisymmetric Laplace equation in spherical coordinates. This should have been straightforward, since we had already learned it in E&M. However, the boundary condition was given as cos^5 θ, whereas I had only memorized Legendre polynomials up to fourth order.
Overall, the computational workload of the exam was extremely heavy. The exam would have been much more interesting if it had emphasized more technique-based methods. For example, special cases of the Frobenius method, more advanced Laplace transform techniques, and generating-function–based integral tricks and inequality arguments that appeared in the homework.
After the midterm, the course focused more on the analytical aspects of ODE. The began with a section from [Hale] on linearized systems, followed by existence and uniqueness of solutions with the contraction mapping theorem from [KBO]. From these, we learned about the characterization of stability, including globalness and asymptotic (Lyapunov) stability of solutions. Up until now I have scored basically full marks for each homework set, which contributes a lot to the semester score. Then I got some points deducted in HW8, where the problem asks us to show the following:
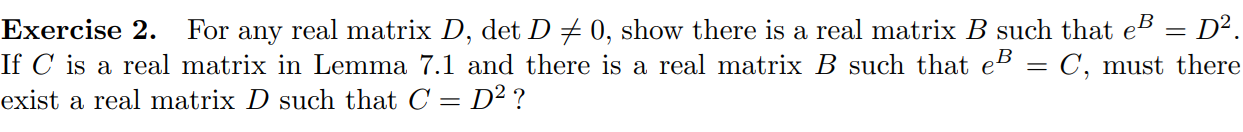
My original solution involved writing down the Jordan form of the relevant matrix and manipulating the eigenvalues, so that I obtain the Jordan form of the logarithm of the squared matrix. However, it was pointed out that the Jordan form may be in fact complex, and my proof did not establish the reality nor the existence of the logarithm. After consulting the TA and classmates, I learned the problem could be solved with the Real Jordan Matrix Theorem. Finally, we covered nonlinear systems, their stability, and phase portrait methods. This part is a lot more familiar to me, so apart from a section from [Hale] on the characterization solutions to ODEs, most materials were not new. This part included classifying fixed points, periodic orbits, limit cycles, attractors etc., and the omega limit set which appeared in the final exam. Also, we introduced the Bendixson-Dulac theorem for falsifying periodic orbit solutions.
The final exam consisted of only 6 problems, but none of which were closely related to the materials covered in the second half of the semester. The first problem asked us to produce an analytic solution to the ODE y’’= 2 sinh y subject to an initial condition and a boundary condition. This seems to be the steady state of a diffusion PDE from biology, and happens to be the few that is solvable. I reduced the problem to solving an integral, but was not able to compute the integral exactly. The second problem asked us to compute solution to a system of first-order ODEs, but the second subproblem was not diagonalizable, so I did not know how to solve it systematically. The third problem was a differential inequality that had not appeared before, but it turns out I did not know the notation used (C^\infty_0 on (-1,1)) implied the space of functions that “vanish on the endpoints”, and so assumed the problem statement was incorrect. The fourth and sixth problems were easier, as one involved exponentiating a matrix to solve a system of ODEs, and the other was Laplace transform.
Unlike geometry, the exams were as difficult as Professor Lin hinted, so I went somewhat prepared to not be able to finish all the problems. In the near future, I plan to organize the midterm and final exam problem and solutions in LaTeX (you are welcome to beat me for forgetting about this). At the end of the semester, I joined the winter reading club on the book Multiple Time Scale Dynamics, which will hopefully make my time at UWaterloo more occupied.
For more details, you may see this post.
Introduction to Geometry 幾何學導論
Lecturer: Professor 郭孝豪
Grade: :/
Department: MATH
Credit(s): 4
Materials:
- Do Carmo, Manfredo Perdigão (2016). Differential Geometry of Curves and Surfaces 2e [Curves&Surfaces]
- Do Carmo, Manfredo Perdigão Riemannian Geometry [Riemann]
The course is graded based on 12 homework sets, a midterm, and a final exam, and the examed material followed Do Carmo’s [Curves&Surfaces]. Despite this, the lecture materials did not follow any particular textbook, but was probably inspired by a mixture of [Riemann] and Differential Geometry by O’Neil especially during the section on affine connectons, connection forms, and Riemannian curvature tensor.
We began the semester with the definition of parametrized curves in 3D space, curvature, torsion, and the Frenet-Serret frames. This section involved tedious calculations, but everything was manageable and straightforward. Then we talked about (regular) surfaces in 3D, proved various criteria on the regularity of surfaces, and talked about diffeomorphisms and homeomorphisms between surfaces, tangent spaces, the first and second fundamental forms, the shape operator, area, and a bit of oriented surfaces. In the midterm exam, the problems were easier than we expected, with 15% of the mark given just for writing down the definition of a regular surface. However, when showing the area-preserving property of the Mercator projection, I used the stereographic projection to brute force the area integral and failed, losing some points for that.
After the midterm exam, the lectures started to get more involved. Professor Kuo introduced 1-forms and, in particular, the connection form. In chapter 3 (at least that is what the homework problems seem to tell us), we talked about the definition of the Gauss map and normal curvature, linking surface properties to the properties of curves that lie on it. Next, the idea of vector fields on surfaces was introduced, mostly following [Curves&Surfaces]. In chapter, isometry and conformal mapping were introduced, and after that lectures started to become a bit incomprehensible for me. Professor Kuo used the language of Riemannian geometry to introduce the Theorema Egregium and the Gaussian equation, writing the Gaussian curvature, or, similarly, the determinant of the shape operator, in terms of differential of the connection form. From that the general version of the Brioschi formula was derived, without the orthogonality assumption. In the TA lectures, the TAs introduced us to manifolds and regular surfaces in higher dimensions, as well as generalized various definitions such as fundamental forms to arbitrary dimensions. Then geodesic curvatures, paralle transport, Christoffel symbols (or connections) were introduced, paralleling many ideas in relativity. Finally, topological theorems and the Gauss-Bonnet Theorem were introduced, including the concept of triangularization, the Euler-Poincaré characteristic, and the Poincaré–Hopf theorem. This part felt most interesting to me, especially the derivation of Gauss-Bonnet and its relation to topological invariants.
Despite doing well in the midterm and all homeworks, I didn’t do well in the final and scored only average. This was probably due to a combination of recklessness and not devoting enough time to the definitions. For example, I would not have lost points on the question about computing geodesic curvature if I recalled correctly that the parallel of a surface of revolution is exactly a circle, and had calculated the normal curvature correctly. Yet another example, if I had inspected carefully, I would have found my errors when calculating the Gaussian curvature and applying the Gauss-Bonnet Theorem. For some reason I had expected the final exam to include some lecture material on Riemannian geometry and high-dimensional surfaces, for example calculating Christoffel symbols for a high-dimensional manifold.
While working through the homework problems, which were picked from [CUrves&Surfaces], I compiled a solution set for the textbook, including problems I found useful or interesting. For more details, you may see this post.
Modern Poetry of Taiwan 臺灣現代詩
Lecturer: Professor 劉正忠
Grade: A
Department: 通識
Credit(s): 2
Materials:
- Self-prepared slides and handouts
Professor Liu introduced us to Taiwanese poets from various times and themes, starting from poem in newly founded Republic of China to Japn-ruled Taiwan, and classic poems to more colloqial poems. Many unexpected topics were introduced throughout the semester, including but not limited to prose poems (散文詩), political poems (政治詩) in the time of and after the lifting of Martial Law, “city poems” (城市詩), gay poems (同志詩), feminist poem (女性詩), cynical poems (厭世詩), and, in the last lecture, AI and lyric poetry. All of these were very interesting, and the professor is a cool perosn. In fact, he is the author of the famous (?) poem on the Taipei City MRT:

Some say this is actually a parody of Chen Ku (顧城)’s poem:

In the final exam, a section asked us to give some thoughts on how the lesson may be made better in the future. I sugegsted including poems by Mu Yang (楊牧) and some non-Mandarin poems, such as poems written in Hakka, Taiwanese, or indigenous languages. For my midterm homework, which asked us to do something “poetry-related” and upload it to COOL, I submitted a poem I wrote a while ago and a handwritten card with the poem written on it. Sadly, due to the length limit on the card, I could only submit one of the four sections of the whole poem.
Nonlniear Optics 非線性光學
Lecturer: Professor 孫啟光
Grade: audit
Department: EE GRAD
Credit(s): 3
Materials:
- Self-prepared notes
The course started by introducing simple terminologies in physical optics, before diving into nonlinear correction terms. I self-studied the notes provided by the professor, and so did not show up to many of the classes in the middle of the semester. Toward the end of the course, double Feynman diagrams were introduced, which are used as a shorthand notation for writing down specific ways in which light-matter interaction happen. In preparing for the midterm presentation for Fundamentals of Experimental Physics, I was puzzled over how to explain a parametric process in optics. Naively, a parametric process is a process whose properties are “parametrized”, in that “something is changing continuously in response to some continuously changing parameter”. This is an extremely vague characterization, but also easily formulated mathematically. However, it turns out a parametric process is an energy- and momentum-conserved process, whereby matter returns to the original quantum state after light-matter interaction, and this manifests in their double Feynman diagrams.
Summary
Overall it is unfortunate I did not do well in the geometry final, but I did learn a lot during the course anyway, and would have done a lot better had I slowed down and focused. Apart from this, I also found the course on Taiwanese Poetry very fulfilling, and I still keep the handwritten card written for the midterm homework under my desk.
